안녕하세요.
고등학교만 졸업했으면 이해할 수 있도록 벡터 해석을 포스팅 해보겠습니다.
우선, 고등학교 때 기본적인 벡터 합,내적 및 외적까진 다 배우잖아요? 그 이후부터 시작할게요.
1. 델 연산자

델 연산자는 이렇게 생겼습니다. x,y,z축에 대해 미분을 한다고 생각하시면 되요.
즉, 기본적으로 델 연산자는 공간에 대해 미분을 하기 위해 사용하는 "미분 연산자"입니다.
(1) 기울기(gradient)
스칼라 함수와 델 연산자를 곱하면, 기울기를 의미하게 됩니다.
너무나 당연하죠? y=x^2이라는 스칼라 함수를 미분하면 y'=x라는 기울기를 찾게 되는거랑 같은거에요.
델 연산자는 스칼라 함수와 만나면 기울기가 됩니다.

(2) 발산(Divergence)
벡터함수에 델 연산자를 내적하면, 발산을 의미하게 됩니다.
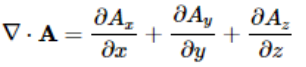

1) A벡터의 발산 값이 0일 때(Div A = 0)
어느 한 곳에 모이거나 퍼지는 것 없이 그저 A벡터는 자신의 방향과 크기만을 가질 뿐입니다.
2) A벡터의 발산 값이 양수일 때(Div A >0)
A벡터가 어느 한 곳에서 퍼져나가는 형태입니다.
3) A벡터의 발산 값이 음수일 때(Div A <0)
A벡터가 어느 한 에서 모이는 형태입니다.

(+)전하는 주변 환경보다 전위값이 높기 때문에 (+)전하로부터 전기장 E가 퍼져나가는 형태를 띄게 됩니다.
(-)전하는 주변 환경보다 전위값이 낮기 때문에 (-)전하로부터 전기장 E가 모이는 형태를 띄게 됩니다.
발산 값이 의미하는 것이 어떤건지 설명하겠습니다. 아래 그림은 적절한 예시가 있어서 퍼왔습니다.

이 벡터는 발산값이 얼마일까요? 0? 양수? 음수? 정답은 양수입니다.
[그림 1]만 보고 발산을 이해하신 분들은 왜 "0"이 아닌 지 의아하실 것입니다.
발산은 어느 한 "점"에서 모이고 퍼지는 것을 의미하는 것이 아닙니다. "점, 선, 면, 부피" 다 가능합니다.
[그림 3]은 "x=0"이라는 "선"을 기준으로 퍼져나가는 것입니다.
발산값에 대한 정확한 의미는 "어느 한 곳에서 멀어지면서 점점 더 쎄게, 혹은 점점 더 약하게 퍼져나가는 정도"라고 이해하시면 될 것입니다. [그림 3]은 오른쪽으로 갈 수록 벡터값이 점점 더 커지죠? 따라서 발산값이 양수가 되는 것입니다.
4) 발산 정리 (Divergence Theorem)

위 수식은 발산정리를 나타냅니다. 발산정리의 물리적 의미를 알아보기 위해 우선 수식을 해석해봅시다.
좌항은 A벡터를 어느 한 부피 v로 둘러싸서 적분한다는 의미입니다.
우항은 A벡터를 어느 폐곡면 S로 둘러싸서 적분한다는 의미입니다.
이 두개가 "="이라는 기호를 통해서 같다고 말하고 있네요.
무슨 의미인지 그림으로 표현해보겠습니다.

어떤 이상한 공간도형이 있다고 칩시다. 그 도형의 부피는 V이고, 표면적은 S입니다.
그런데 그 도형 내부 p점에 연막탄이 하나 있다고 해봅시다. 그럼 p점에서부터 가스가 막 퍼져나가겠죠?
그 가스가 A벡터인거에요. 가스는 p점에서부터 일정한 속도로 퍼져나갈거고 결국 이 도형의 표면적인 S에 부딫혀서 갇히게 되겠죠.
가스 A의 이동 속도는 "div A"가 되는거에요.
발산정리의 의미는 "가스가 퍼지고 있는 어느 한 시점에, 이 공간 내부의 가스 이동속도를 싹다 구해서 더하면 결국 현재 표면적 S에 있는 가스의 총 량과 같다"는 의미입니다. 시간에 대해서 정의한 것 아니에요! 공간에 대해 정의했기 때문에 시간은 멈춰둔 상황이라고 보셔야해요. 가스가 퍼져나가는 중입니다.
발산정리를 수학적으로 증명은 따로하지 않겠습니다. 이런 물리적인 의미만 외워두시면 됩니다.
(3) 회전 (Curl)
벡터함수에 델 연산자를 외적하게 되면, 회전을 의미합니다.

수식만 보면 복잡하죠? 하지만 그림을 보면 이해하기 쉬우실 겁니다.

얘가 회전이에요. 말그대로 회전하는겁니다. 한바퀴 쭉 도는거요. 그래서 벡터가 한바퀴 도는 형태이면 Curl A는 어느 값을 가지게 됩니다.

Divergence와 Curl을 잘 표현해둔거라 퍼왔습니다.
Curl값이 양수이면 벡터 A가 반시계방향으로 회전하는 것입니다. 음수이면 시계방향으로 회전하는 것이구요.
Curl이 "0"이면, 회전하는게 없다는 뜻이겠죠?
Curl의 절대값이 크면 클수록 회전 속도가 빠르다는 의미입니다.
1) 스토크스 정리

우항의 의미: 폐곡면 S 내부의 Curl F값을 모두 더한다.
좌항의 의미: 폐곡선 C를 따라서 벡터함수 F를 모두 더한다.
자 그럼, 이 두개가 같다는 의미는 도대체 어떤 뜻일까요?
"폐곡면 S 내부의 회전력을 모두 더하면 해당 폐곡면의 경계인 C를 따라 F값을 다 더한 것과 같다"는 의미입니다.
아래 그림을 보면 이해가 더 잘 될거에요.

즉, 내부 회전을 다 더하면 결국 테두리의 회전과 같다는 의미! 참 쉽죠?
(4) 라플라시안
라플라시안은 델 연산을 2번한 것입니다. 정확히 말하면 기울기의 발산값을 구한 것이에요.

스칼라함수의 라플라시안과 벡터함수의 라플라시안을 나눠서 해석해보겠습니다.
1) 스칼라함수의 라플라시안

스칼라함수의 라플라시안을 구한다는 것은, 해당 함수의 기울기가 급변하는 곳이 있는지 찾는다는 의미입니다.

사진의 경우엔 배경과 인물 사이에 색깔 값이 크게 확 변하죠? 색깔 함수에 대해 라플라시안을 구하면 위 예시처럼 윤곽을 따낼 수가 있습니다.

저렇게 기울기가 확 변하는 변곡점들 있죠? 그걸 찾는게 "라플라시안"이라고 보면 되겠습니다.
2) 벡터함수의 라플라시안
벡터함수에서도 기본적인 의미는 같습니다. 다만 계산 방법만 달라서 해당 항등식을 소개하도록 하겠습니다.

3) 라플라시안과 관련된 방정식의 의미
라플라시안 연산자를 활용한 방정식은 4가지 경우에 대해 물리적인 의미만 이해하고 넘어가는 것으로 하겠습니다.
- 라플라스 방정식(Laplace equation)

라플라스 방정식은 라플라시안 값이 "0"일 때를 의미합니다. 경계조건을 세워야 구체적인 값을 구할 수 있지만, 결론부터 말하자면 "조화함수"를 해로 갖고 있습니다.
좁은 의미로 말하자면, Harmonic을 갖는 sin, cos파를 의미합니다.
- 푸아송 방정식(Poisson's equation)

푸아송 방정식은 라플라시안 값이 "상수"일 때를 의미합니다. 전자기학에선 특정 전하량을 갖는 스칼라 퍼텐셜을 구할 때 사용됩니다.
사실 푸아송 방정식과 라플라스 방정식을 풀기 위해서는 경계조건을 줘야합니다.
해당 영역 밖의 영향에 대해서도 고려해야 문제를 풀 수 있단거죠.
경계조건은 크게 2가지가 있습니다.
- 노이만 경계조건: 경계에 미분 값을 주는 것.
- 디리클레 경계조건: 경계에 함수 값을 주는 것.
- 확산 방정식(Diffusion equation)
라플라시안 값이 미분값으로 나오는 경우를 의미합니다. 열확산 운동(브라운 운동)이나 반도체 소자 PN접합의 캐리어 확산 해석 등에 분자의 이동에 대해 해석할 때 사용됩니다.

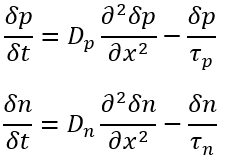
- 파동 방정식(Wave equation)
파동 해석에 사용됩니다. 전자기학에서는 전기장과 자기장의 시간에 따른 변화, 즉 시변전자기장(=전자기파)을 해석할 때 사용됩니다.

2. 중요한 벡터 항등식
(1) 계산에 유용한 벡터 항등식

(2) 중요한 물리학적 의미를 갖는 벡터 항등식

첫번째 것은 의미가 너무 쉽습니다. 회전은 말그대로 주변을 도는 것인데 발산값은 당연히 "0"이 되겠죠?
세번째 것 역시 당연합니다. 기울기 값이 있다는 것은 회전이 아니라는거죠.
이를 활용한 것이 2번째와 4번쨰 항등식 입니다.

발산하지 않으면 그 벡터는 회전한다! 이를 활용해서 전자기학에서 꽤 많은 해석을 하니까 꼭 알아두시길 바랍니다.
다음으로는,

회전하지 않는 벡터는 "기울기 연산자"로 표현된다!
여기까지만 알면 전자기학을 이해하는데는 아무런 문제가 없습니다.
그럼 다음 포스팅에서는 정전기장에 대해 알아보도록 하겠습니다.
'전자기학' 카테고리의 다른 글
| 가우스 법칙 전기장에서의 일과 에너지 (2) | 2025.02.01 |
|---|---|
| 쿨롱의 법칙과 전계, 전위, 일과 에너지 (0) | 2025.01.29 |
| 전자기학 전자책 pdf 출시 (0) | 2023.07.31 |
| 정전기학(Electrostatics): 내용 소개 (0) | 2023.03.25 |
| 전자기학 포스팅 순서 (0) | 2023.02.11 |