안녕하세요.
다른 포스팅에서 말씀드렸듯이 전자기학 전자책을 크몽에서 판매 중입니다.
블로그 주제를 조금 더 다양하게 넓혀보고자, 해당 전자책을 활용해서 전자기학 관련 포스팅을 하고자 합니다.
본 포스팅에서 사용되는 이미지는 모두 전자책 내용에서 발췌하였습니다.
전자책 구입은 아래 링크에서 가능하오니 많은 관심 부탁드립니다!
https://kmong.com/self-marketing/491492/ObFbhG4KJw
7,9급 공무원, 공기업, 학점관리용 전자기학 필기노트 - 크몽
뽀대컴퍼니 전문가의 자료·템플릿 서비스를 만나보세요. <p>저는 국내외 학회에서 다수의 논문을 냈으며, 지금도 H대기업 연구원으로서 관련 직종에...
kmong.com
전자책 내용은 필기노트 형식으로 작성되어서 요약 정리된 내용 위주이며, 본 블로그 포스팅과 함께 보시면 더욱 도움이 될 것이라 생각합니다.
유전체(Dielectric Materials)는 전기장이 가해질 때 내부적으로 자유전자의 흐름이 아닌, 전하 분포의 재배열을 통해 반응하는 물질입니다. 이러한 현상은 분극(Polarization) 이라고 불리며, 유전체 내부에서 속박전하(Bound Charge) 가 형성되는 원인이 됩니다.
속박전하는 유전체 내부의 전하 재배열로 인해 발생하며, 이는 물질의 전기적 특성, 전계 분포, 커패시턴스, 유전율 등과 직접적으로 관련됩니다. 특히, 분극이 균일한 경우와 불균일한 경우 속박전하의 분포가 다르게 나타나며, 이에 따라 전기장 해석이 달라질 수 있습니다.
이번 글에서는 유전체 내에서 속박전하가 형성되는 원리와 분극이 균일한 경우와 불균일한 경우의 차이를 전문가적인 시각에서 심층적으로 분석해보겠습니다.
1. 유전체 속박전하란 무엇인가?
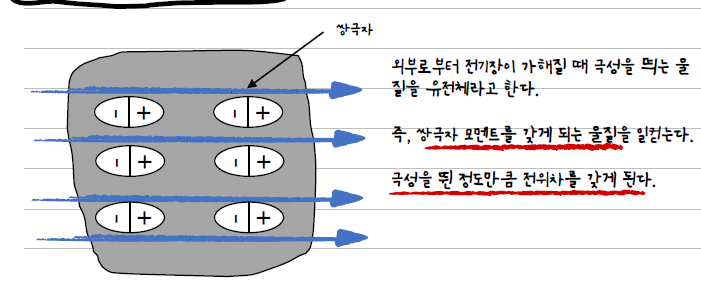
유전체가 전기장에 노출되면, 내부의 원자 혹은 분자가 반응하여 전자의 확률적 분포가 이동하면서 쌍극자(Dipole)가 형성됩니다.
즉, 물질 내부에서 전하가 자유롭게 이동하는 것이 아니라, 전하 중심이 미세하게 변형되면서 국소적인 전하 밀도가 형성되는 것입니다.
이때 형성되는 전하는 크게 속박전하(Bound Charge) 와 자유전하(Free Charge) 로 나뉩니다.
- 자유전하(Free Charge): 금속에서 볼 수 있는 자유롭게 이동하는 전하 (도체 내부에서는 이러한 자유전하가 존재함).
- 속박전하(Bound Charge): 유전체 내부에서 분극으로 인해 형성된 전하.
속박전하는 다시 두 가지로 구분됩니다.
1) 표면 속박전하 (Surface Bound Charge)
: 유전체 표면에서만 발생하는 속박전하로써, 분극 벡터(P)의 법선 성분에 의해 결정됩니다.
$$\sigma_P = P(r') \cdot \hat{n}$$
2) 부피 속박전하 (Volume Bound Charge)
유전체 내부에서 발생하는 속박전하로써, 분극이 공간적으로 변화할 경우 나타납니다.
$$\rho_P = -\nabla \cdot P(r')$$
위 식은 부피 속박전하 밀도의 정의입니다. 이를 해석하면, 분극의 균일성에 따라 발산 여부가 결정된다는 것이며,
이것이 곧 속박전하의 형성 여부가 결정된다는 의미입니다.
즉, 속박전하는 단순히 전기장이 존재한다고 해서 무조건 발생하는 것이 아니라, 유전체 내부에서 분극의 형태가 어떻게 변화하는가에 따라 다르게 나타납니다.
지금까지 어렵게 속박전하(Bound Charge)라고 말했지만, 쉽게 말하면 분자의 배열입니다.
외부 전기장에 가해졌을 때, 분자가 나란히 배열되는 경우에는 분자들의 극성이 서로 상쇄되어 양 끝단에 분극만 형성될 거에요. 그것을 "표면 속박전하"라고 합니다.
그러나 분자가 나란히 배열되지 않는 경우에는 분자들의 극성이 서로 상쇄되지 않을 것이고, 유전체의 체적 내에도 일부 극성을 형성하게 될건데 이를 "부피 속박전하"라 합니다.
2. 분극의 균일성과 속박전하 분포의 차이
속박전하의 분포는 유전체 내부에서 분극(Polarization, P)이 균일하게 형성되는가, 아니면 불균일한가에 따라 크게 달라집니다.
(1) 분극이 균일한 경우 (Homogeneous Polarization)
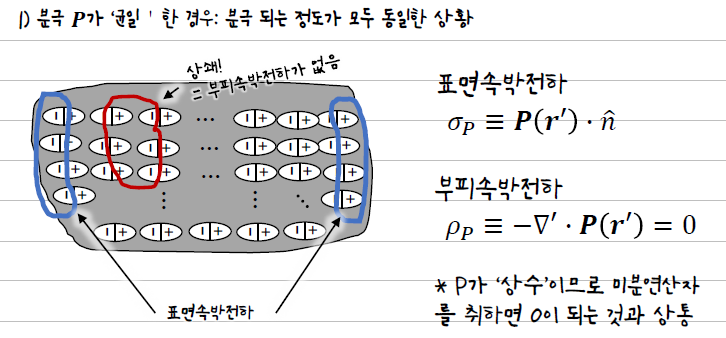
유전체 전체에서 동일한 정도로 분극이 발생.
분극 벡터 P가 일정한 값을 가지므로, 발산이 0이 됩니다.
결과적으로 부피 속박전하가 0이 되어, 유전체 내부에는 속박전하가 존재하지 않음.
다만, 유전체의 표면에서는 전기장의 방향에 따라 속박전하가 형성됨.
$$\rho_P = -\nabla \cdot P = 0$$
$$\sigma_P = P \cdot \hat{n}$$
즉, 속박전하는 유전체의 표면에만 존재하고 내부에는 형성되지 않음.
균일한 분극에서는 내부 속박전하를 고려하지 않아도 되며, 표면에서만 속박전하가 존재합니다.
(2) 분극이 불균일한 경우 (Non-Homogeneous Polarization)
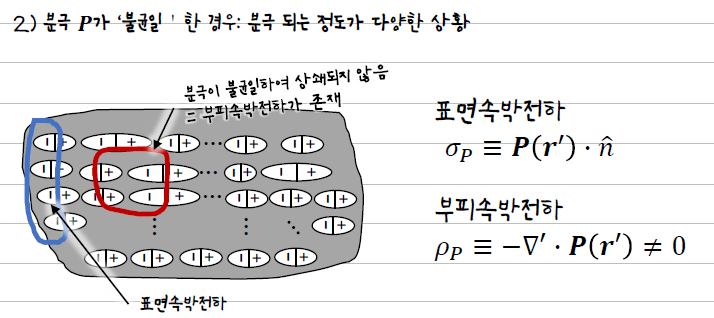
유전체 내부에서 분극의 크기 또는 방향이 공간적으로 다르게 나타남.
분극 벡터 P의 변화율이 0이 아니므로, 발산이 0이 아님.
따라서 부피 속박전하 ≠ 0 이 되어, 유전체 내부에서도 속박전하가 형성됨.
표면 속박전하도 함께 존재할 수 있음.
$$\rho_P = -\nabla \cdot P \neq 0$$
즉, 속박전하는 유전체 내부에서도 존재할 수 있으며, 전기장 해석에서 이를 반드시 고려해야 함.
불균일한 분극 상태에서는 내부의 부피 속박전하까지 고려해야 함.
3. 유전체 속박전하의 해석적 중요성
1) 유전체 내부 전기장의 해석
속박전하는 유전체 내부의 전기장을 결정하는 핵심 요소 중 하나입니다. 특히, 균일한 분극과 불균일한 분극을 구별하여 해석하는 것이 중요합니다.
- 균일한 분극 → 표면 속박전하만 고려하면 됨.
- 불균일한 분극 → 부피 속박전하도 고려해야 함.
2) 전기용량(Capacitance) 및 유전율(Dielectric Permittivity) 분석
유전체 내부의 속박전하는 커패시터(Capacitor)의 전기용량에 직접적인 영향을 미칩니다.
- 부피 속박전하가 존재하면 내부 전계가 변형됨 → 유전율이 공간적으로 달라질 수 있음.
- 이는 유전체를 활용한 다양한 전자 소자의 성능을 결정하는 중요한 요소.
3) 전기장 경계 조건(Boundary Conditions) 적용
속박전하를 고려하면 전기장의 연속성과 경계 조건을 정확하게 계산할 수 있음.
- 예를 들어, 유전체 경계에서 전속밀도(D)와 전기장(E)의 불연속성을 해석할 때 속박전하의 분포를 반드시 반영해야 함.
정리
1. 유전체가 전기장 내에서 균일하게 분극되는 경우 표면에만 속박전하가 형성된다.
2. 유전체가 전기장 내에서 불균일하게 분극되는 경우에는 표면과 함께 부피 내에서도 속박전하가 형성된다.
'전자기학' 카테고리의 다른 글
| 유전체 내부에서의 전속밀도와 전기장: 속박전하의 영향 (0) | 2025.03.12 |
|---|---|
| 물질 속의 전기장과 전위 (1) | 2025.03.05 |
| 함수의 내적과 직교성, 푸리에 급수 (0) | 2025.03.04 |
| 다중극 전개: 왜 하필 르장드르 다항식일까? (0) | 2025.03.03 |
| 다중극 전개: 홀극자와 쌍극자의 물리적 특성 비교 (0) | 2025.03.03 |